Kluczowa różnica : W rachunku różniczkowym jest proces, według którego ustala się szybkość zmiany krzywej. Integracja jest przeciwieństwem różnicowania. Podsumowuje on cały mały obszar leżący pod krzywą i dowiaduje się o całkowitej powierzchni.

Różniczkowanie i integracja to dwa podstawowe elementy rachunku różniczkowego. Rachunek różniczkowy i rachunek całkowy są dokładnie odwrotne względem siebie. Rachunek różniczkowy w zasadzie zajmuje się procesem dzielenia czegoś w celu śledzenia zmian. Z drugiej strony, rachunek całkowy dodaje wszystkie elementy razem.

Zróżnicowanie dotyczy obliczania pochodnej, która jest chwilową stopą zmiany funkcji uwzględniającą jedną z jej zmiennych. Zajmuje się ilościami, które ciągle się różnią. Innymi słowy, jest to odpowiednik nachylenia linii stycznej, którą reprezentuje m = zmiana y / zmiana w x.

Można to zrozumieć na podstawie tego przykładu - jeśli istnieje funkcja f (x) posiadająca niezależną zmienną x, to w przypadku, gdy x jest zwiększane o małą wartość, która byłaby delta x. Następnie ta sama zmiana zostanie odzwierciedlona w funkcji również jako delta f. Współczynnik delta f / delta x oblicza tę szybkość zmiany funkcji względem zmiennej x.

Integracja jest przeciwieństwem różnicowania i dlatego jest również określana jako antyróżnicowanie. Jest w stanie określić funkcję pod warunkiem, że jest pochodną. Mierzy obszar pod funkcją między granicami. Proces integracji jest nieskończonym sumowaniem iloczynu funkcji x, która jest f (x) i bardzo małej delta x. W kontekście krzywej zapewnia całkowity obszar pod krzywą od osi x do krzywej z określonego zakresu. Jest on przedstawiony symbolem ∫. Jeśli wspomniany jest określony przedział, to jest znany jako całka oznaczona, inaczej całka nieoznaczona.

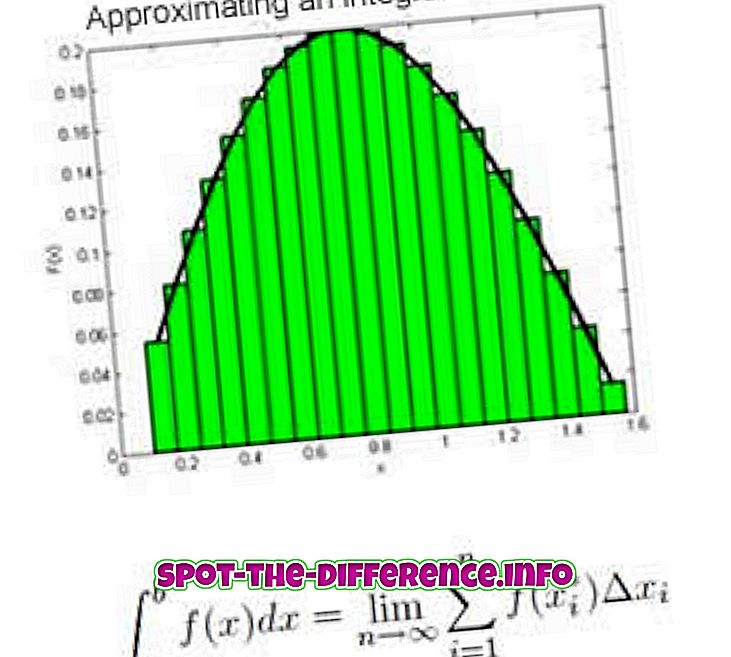
Ponieważ integracja i różnicowanie są po prostu odwrotne względem siebie, integracja może zapewnić oryginalną funkcję, jeśli znana jest pochodna. Jest również opisane jako podstawowe twierdzenie rachunku różniczkowego. Różnice dotyczą różnic i podziałów, podczas gdy integracja polega na dodawaniu i uśrednianiu. Różnica określa funkcję nachylenia, ponieważ odległość między dwoma punktami staje się bardzo mała, podobnie proces integracji określa obszar pod krzywą, gdy liczba partycji prostokąta leżących pod krzywą staje się duża.

Porównanie różnicowania i integracji:

	Różnicowanie	Integracja
Różnica	Służy do znalezienia zmiany funkcji w odniesieniu do zmiany wejścia	Odwrotny proces lub metoda różnicowania
Oparte na	Działowy	Integracja
Określa	Prędkość funkcji	Odległość przebyta przez funkcję
Wykres	Nachylenie funkcji	Obszar między funkcją a osią x
Przykład	Dla y = x do potęgi 4 dy / dx = 4 (x podniesienie do potęgi 3)	Integracja 4 (x podniesienie do potęgi 3) jest równa = x do potęgi 4
Formuła	Pochodna funkcji f (x) w odniesieniu do zmiennej x jest zdefiniowana jako	Definicja całki f (x) z [a, b]
Podanie	Aby określić, która funkcja rośnie lub maleje, obliczamy chwilową prędkość	Służy do znajdowania obszarów, objętości, punktów centralnych itp