Kluczowa różnica: Okrąg i elipsa mają zamknięte zakrzywione kształty. W kole wszystkie punkty są jednakowo oddalone od środka, co nie ma miejsca w przypadku elipsy; w elipsie wszystkie punkty znajdują się w różnych odległościach od centrum.
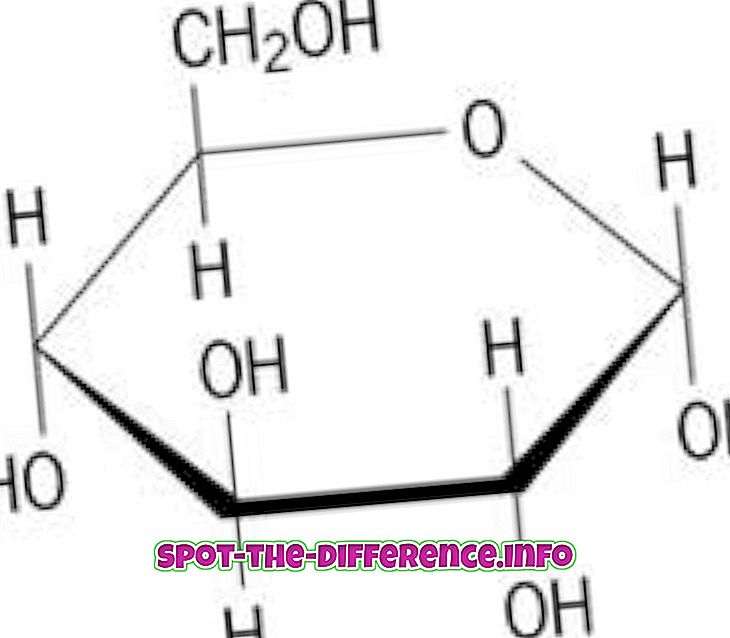
Matematycznie okrąg jest głównym kształtem w dziedzinie geometrii, a jego definicja mówi: okrąg to kształt z wszystkimi punktami w tej samej odległości od jego środka. Nazwa pochodzi od jego centrum. Niektóre rzeczywiste przykłady koła to koła, talerz obiadowy i (powierzchnia) monety.
Słowo " cyrk " pochodzi od greckiego terminu " kirkos ", który jest metatezą homeryckiej greki i oznacza " obręcz " lub " pierścień ". Koło było znane przed zapisaną historią. Słońce i Księżyc są naturalnymi przykładami koła, podczas gdy nawet krótkie łodygi wiejące na wietrze tworzą kształt koła w piasku. Zasada koła została zastosowana w formowaniu kół i kół zębatych przez człowieka prehistorycznego. Teraz w czasach nowożytnych istnieją rozmaite odmiany maszyn oparte na kształcie koła. Badanie koła i jego rozwój można zastosować w dziedzinie matematyki, geometrii, astronomii i rachunku różniczkowego.
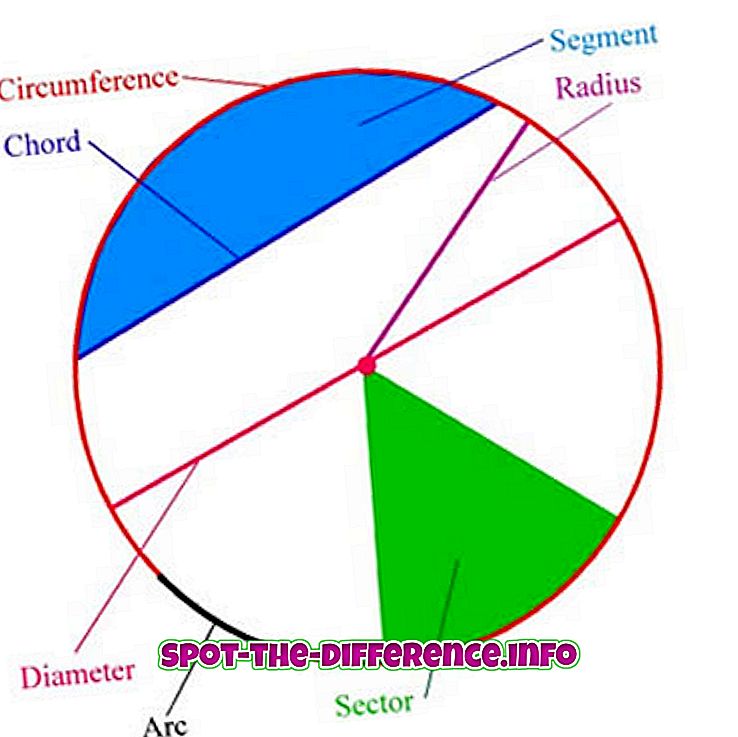
W terminologii koła zaangażowane są następujące terminy:
Łuk : dowolna połączona część koła.
Środek : punkt w równej odległości od punktów na okręgu.
Promień : odcinek linii łączący środek okręgu z dowolnym punktem na samym okręgu; lub długość takiego segmentu, który wynosi połowę średnicy.
Średnica : odcinek linii, którego punkty końcowe leżą na okręgu i przechodzą przez środek; lub długość takiego odcinka linii, który jest największą odległością pomiędzy dowolnymi dwoma punktami na okręgu. Jest to szczególny przypadek akordu, a mianowicie najdłuższy akord, i jest dwa razy większy od promienia.
Obwód e: długość jednego obwodu wzdłuż koła.
Akord : odcinek linii, którego punkty końcowe leżą na okręgu.
Styczna : współpłaszczyznowa prosta, która dotyka okręgu w jednym punkcie.
Półksiężyc e: obszar ograniczony średnicą i łukiem leżącym między punktami końcowymi średnicy. Jest to szczególny przypadek segmentu kołowego, a mianowicie największego.
Sektor okręgowy : obszar ograniczony przez dwa promienie i łuk leżący między promieniami.
Matematycznie elipsa jest powszechnym kształtem w dziedzinie matematyki. Jego definicja określa: zakrzywioną linię tworzącą zamkniętą pętlę, w której suma odległości od dwóch punktów (ognisk) do każdego punktu na linii jest stała. Prawdziwe przykłady elipsy to: hula-hoop, szklanka wody i prosta płyta obiadowa, gdy są przechylone pod kątem.
Apoloniusz z Pergi nadał w swoim Konikom nazwę "elipsa", która podkreśla połączenie krzywej z zastosowaniem obszarów. Jest to krzywa na płaszczyźnie otaczającej dwa punkty ogniskowe, w taki sposób, że prosta biegnąca od jednego z punktów ogniskowych do dowolnego punktu na krzywej, a następnie z powrotem do drugiego punktu ogniskowania ma tę samą długość dla każdego punktu na krzywej. Jego kształt jest reprezentowany przez jego ekscentryczność, która jest arbitralnie bliska 1. Badanie elipsy i jej właściwości jest powszechnie stosowane w dziedzinie fizyki, astronomii i inżynierii. Orbity planet ze Słońcem w jednym z centralnych punktów, księżyce krążące wokół planet i inne układy posiadające dwa ciała astronomiczne są ogólnymi przykładami ścieżek eliptycznych. Kształt planet i gwiazd jest często dobrze opisywany przez elipsoidy. Elipsa jest również uważana za najprostszą figurę Lissajousa, utworzoną, gdy ruchy poziome i pionowe są sinusoidami o tej samej częstotliwości.
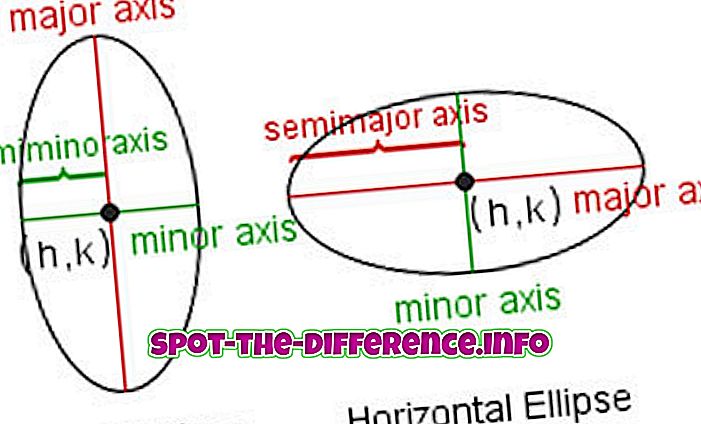
Terminy związane głównie z terminologią elipsy to:
Fokus : odległość od środka i jest wyrażona w kategoriach dużych i mniejszych promieni.
Mimośród : Ekscentryczność elipsy (powszechnie oznaczana jako e lub ε) jest wyrażana w terminach przy użyciu współczynnika spłaszczenia.
Directrix : jest to linia równoległa do osi podrzędnej, z którą powiązane są poszczególne fokusy .
Latus rectum : Pasma elipsy, które są prostopadłe do osi głównej i przechodzą przez jeden z jej ognisk, nazywane są latus rectum elipsy.
Główna / Mniejsza oś : najdłuższa i najkrótsza średnica elipsy. Długość osi głównej jest równa sumie dwóch linii generatora.
Oś pół-wielka / pół-mała : odległość od środka do najdalszego i najbliższego punktu na elipsie. Połowa osi dur / minor.
Akordy : Punkty środkowe zbioru równoległych akordów elipsy są współliniowe.
Obwód : wiąże się z długością osi pół-wielkiej i mimośrodem i jest integralną częścią elipsy.
Porównanie między Circle i Ellipse:
okrąg | Elipsa | |
Definicje | Okrąg jest okrągłą postacią, której granica (obwód) składa się z punktów równoodległych od punktu stałego (środka). | Elipsa to regularny owalny kształt, śledzony przez punkt poruszający się w płaszczyźnie, tak że suma jego odległości od dwóch innych punktów (ognisk) jest stała, lub powstaje, gdy stożek jest przecinany ukośnie, co powoduje nie przecinają podstawy. |
Wariacje | Okręgi nie różnią się kształtem; pozostają one w tym samym kształcie, nawet jeśli widok jest zmieniony. | Elipsy różnią się kształtem od bardzo szerokich i płaskich do prawie okrągłych, w zależności od tego, jak daleko od siebie znajdują się ogniska. |
Promień konsystencji | Ma stały promień w całym kształcie. | Nie ma stałego promienia w całym kształcie. |
Główne składniki | Okrąg ma jeden promień, który leży pośrodku. | Elipsa ma dwa ogniska, które znajdują się na obu końcach. |
Powierzchnia | π × r ^ 2 Gdzie "r" oznacza promień okręgu. | π × a × b Gdzie "a" jest długością osi pół-dur, a "b" jest długością osi półpoślizgowej. |
Standardowe równania | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
Podobieństwo | Kręgi są unikalnymi kształtami, z których pochodzą inne kształty. | Elipsy powstają również jako obrazy koła pod projekcją równoległą i ograniczone przypadki rzutowania perspektywicznego. |