Kluczowa różnica: sekwencja jest uporządkowaną listą liczb lub terminów. Może zawierać elementy, liczby i terminy i może być zbiorem ograniczonym lub zbiorem nieskończonym. Seria z drugiej strony jest sumą sekwencji.
Serie i sekwencje najczęściej słyszy się w matematyce i statystyce. Stanowią one także ogromną część fizyki, informatyki i finansów. Chociaż w języku angielskim są to słowa wymienialne, w matematyce definicja sekwencji i serii znacznie się różni. Sekwencja to po prostu uporządkowana lista liczb lub terminów. Seria jest sumą sekwencji.

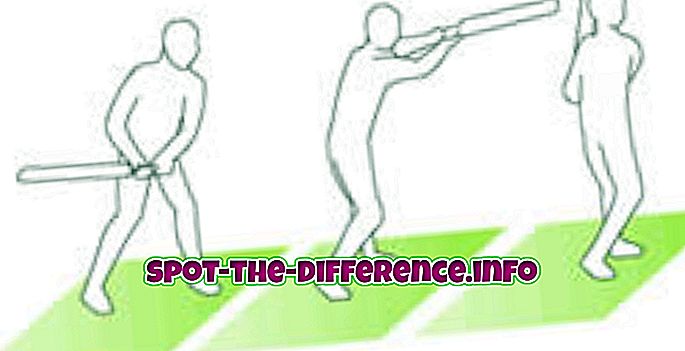
Sekwencja to uporządkowana lista liczb lub terminów. Może zawierać elementy, liczby i terminy i może być zbiorem ograniczonym lub zbiorem nieskończonym. W przeciwieństwie do zestawu kolejność w sekwencji ma ogromne znaczenie. Jest znany jako funkcja dyskretna. Na przykład [1, 2, 3, 4 ...] jest sekwencją lub progresją (w Wielkiej Brytanii). Istnieją dwa typy sekwencji: sekwencja arytmetyczna i sekwencja geometryczna. Sekwencja arytmetyczna jest sekwencją, w której różnica między dwoma kolejnymi pojęciami pozostaje stała, znana jako wspólna różnica. W sekwencji geometrycznej stosunek dwóch kolejnych pojęć pozostaje stały, znany jako wspólny stosunek.
Sekwencje mogą być skończone lub nieskończone, na przykład ciąg wszystkich dodatnich liczb całkowitych (2, 4, 6 ...). Sekwencje skończone są czasami określane jako ciągi lub słowa i nieskończone sekwencje jako strumienie. Pusta sekwencja () jest zawarta w większości pojęć sekwencji, ale może być wyłączona w zależności od kontekstu. Sekwencja może również mieć dostęp do porządku lub kolejności malejącej. Zwykle ma wzór, który można łatwo odgadnąć. Sekwencja może być nazywana lub określana jako "A" lub "A n ". Terminy sekwencji są zwykle nazywane "ai" lub "an", a indeksacja lub licznik to "i" lub "n". Przykład: A2 jest drugim miejscem w sekwencji, a A6 oznacza szóste miejsce w sekwencji.

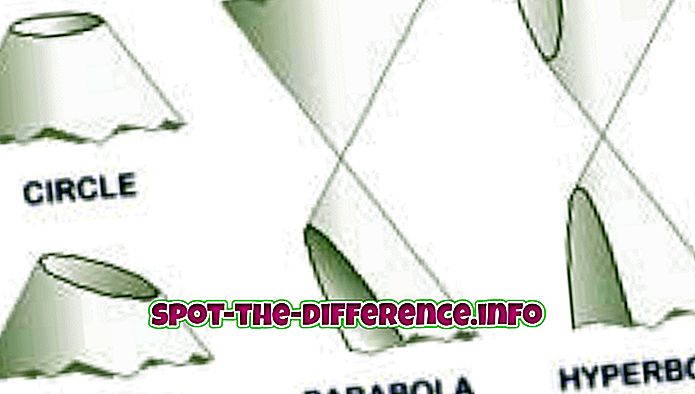
Na przykład sumowanie pierwszych do dziesięciu terminów sekwencji byłoby napisane jako

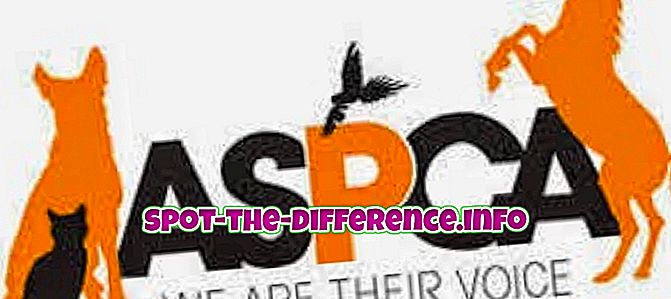
Równanie może być również zapisane w rozszerzonej formie jako:
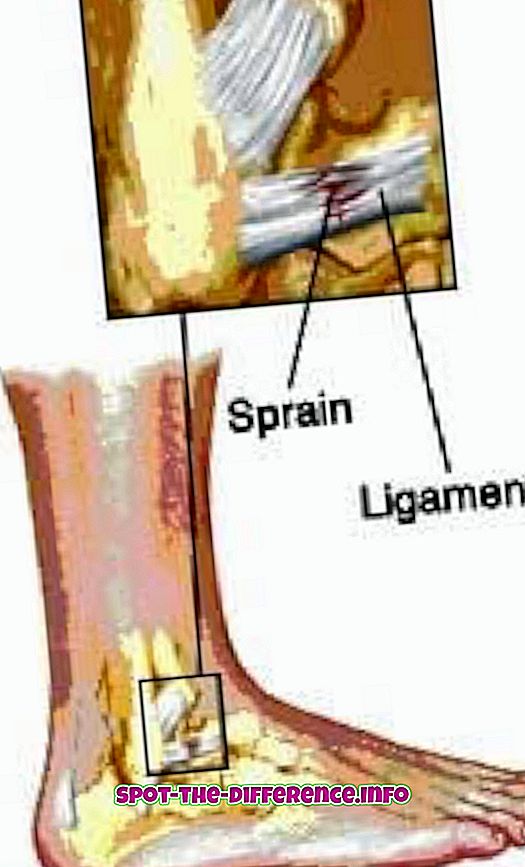
Σ = a1 + a2 + a3 + a1 = 4 + a5 + a6 + a7 + a8 + a9 + a10
Dowolną literę można użyć jako indeksu, a najpopularniejsze to: i, j, k i n.